Tegenvallende resultaten op school en nu?
Op veel scholen zijn deze week de verslagen/rapporten uitgedeeld. Voor de meeste kinderen en ouders een soort bevestiging van(...)
Rekenen in groep 6
Rekenen in groep 6
Zuchtend pakt zoonlief zijn tas uit. Opeens zeilt er een rekenboek en een schrift op tafel.
“Ik had het niet af en moet het nu afmaken, dat ga ik echt niet doen hoor, zo stom”.
Na een stapel boterhammen en een kop thee pakt hij (zij het zwaar zuchtend) zijn rekenboek op. “Dan heb ik het maar af”.
Hij moet wat min en plus sommen maken en dan zelf bedenken welke strategie erbij hoort.
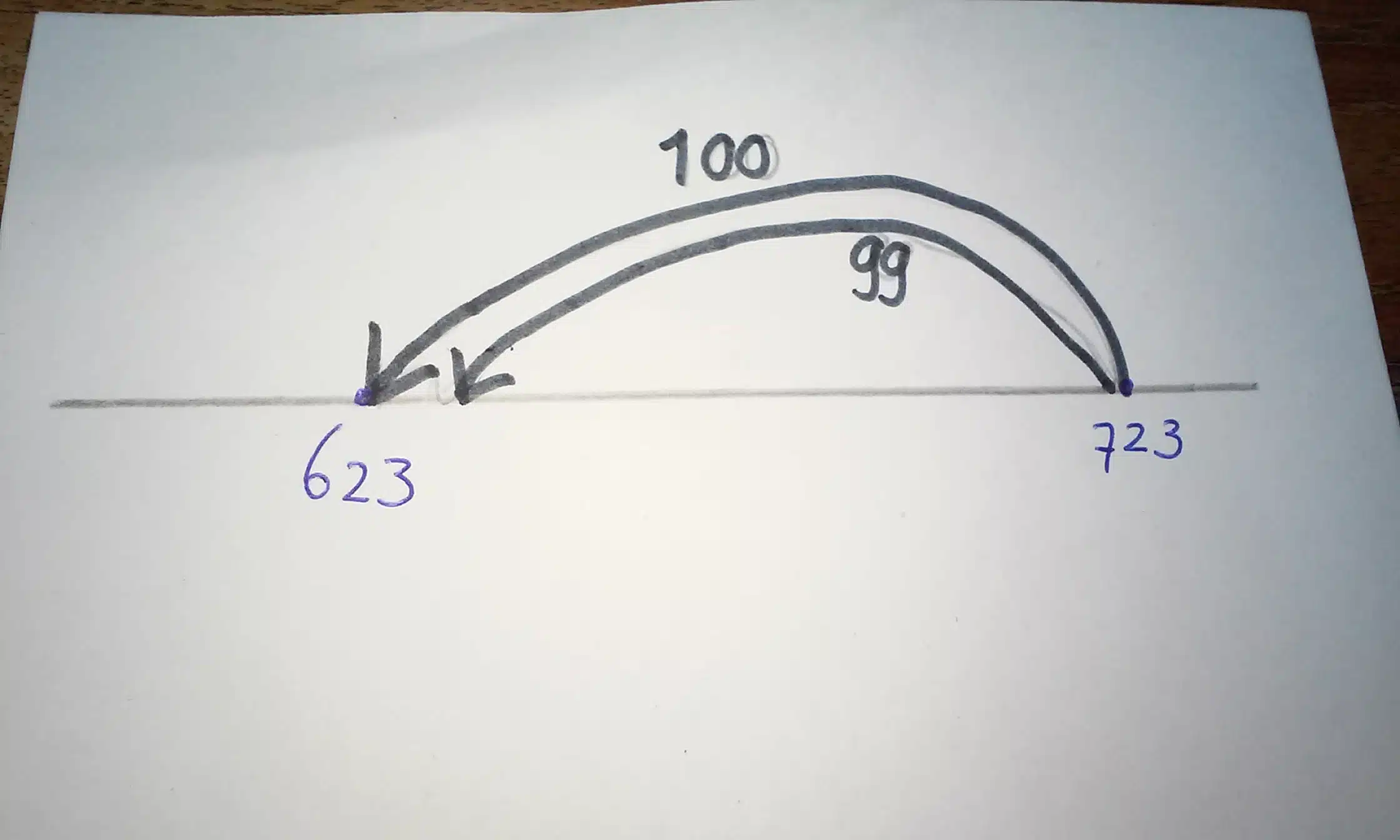
“hee mam, hoe moet dit?” Hij is beland bij de som 723-99
Hij heeft als antwoord: 622
Als verklaring: je doet niet 99 maar 100 en dan eentje meer.
Een mooi riedeltje alleen doet hij er eentje naar links in plaats van naar rechts. Vertellend komen we er niet helemaal uit, hij begrijpt het wel als ik een tekening maak.
Dit valt me vaker op bij leerlingen, ze weten wel ongeveer wat ze moeten doen, maar ze zijn dan het inzicht in de som kwijt. Als ze het tekenen, een overzicht hebben, zien ze wel of ze er nu een naar links of naar rechts moeten.
Het bieden van structuur geeft zwakke rekenaars houvast, duidelijkheid en voorspelbaarheid.
Heel belangrijk hierbij is een gedegen observatie van de strategie die een kind bij rekenen toepast. Hoe pakt een kind een opgave aan, hoe oriënteren kinderen zich op een opgave?
Nemen ze voldoende tijd om de te kijken wat er in de opgave staat?
Daarnaast kan het interessant zijn om te onderzoeken of een kind in staat is om bepaalde gegevens korte tijd te onthouden. Iedere strategie kent immers wel een aantal deelstappen.
Voorbeeld: 80+40= 40=20+20 100+20=120 Hierbij moet de deelhandeling, 40=20+20 even onthouden worden. Sommige kinderen vinden dat moeilijk en vergeten uitkomsten van deelstappen of raken het spoor bijster.
